思い切ってニューラルネットワークを勉強してみよう(3)
※本記事は、未来技術推進協会ホームページにて2018年12月13日に掲載されたものです。
こんにちは。山本睦月です。
前回に引き続き、思い切ってニューラルネットワークを勉強してみようパート3です。
続きからの内容となりますので、パート1と2をご覧になってから本記事に進むのをオススメします。
※前回の記事はこちら
(思い切ってニューラルネットワークを勉強してみよう(1))
(思い切ってニューラルネットワークを勉強してみよう(2))
目次
前回のおさらい
世間が大いに期待した、自分で学習する人工的な装置『パーセプトロンモデル』でしたが、線形分離できない事象を解決できない『XOR問題』が発覚。パーセプトロンモデルが活躍するために解決が必要な課題がまだ残されており、人工知能は冬の時代に突入しました。
パーセプトロンの深層化
前回、パーセプトロンモデルでは線形分離可能な問題しか学習できないと述べました。
実はこのXOR問題に関しては、モデルを少し工夫することで解決が可能なのです。
論理演算の代表的な4つ『①AND②OR③NAND④XOR』の内、①~③を組みわせることで、XORと同じ出力結果を実現できます。順番におさらいしながら見ていきましょう。
-
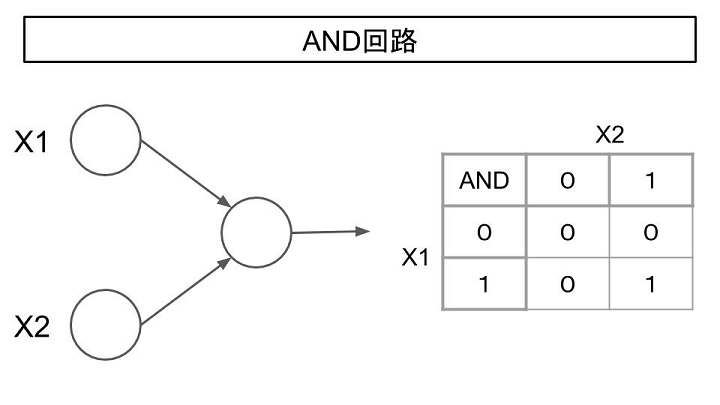
- ①AND回路
AND回路はX1、X2いずれも1が入力された場合のみ1を出力するものです。
-
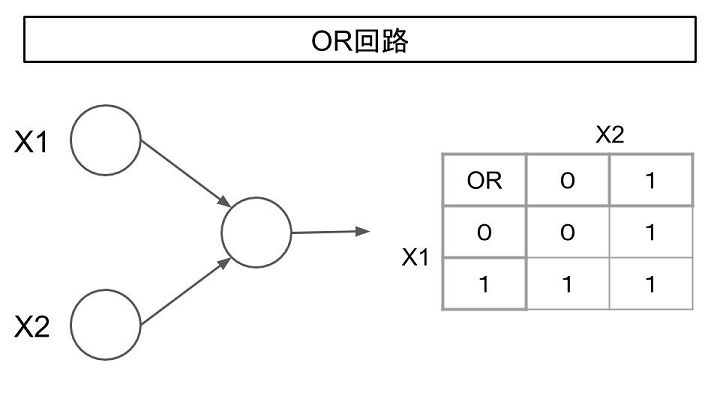
- ②OR回路
OR回路はX1、X2いずれかが1を入力した際に1を出力するものです。
-
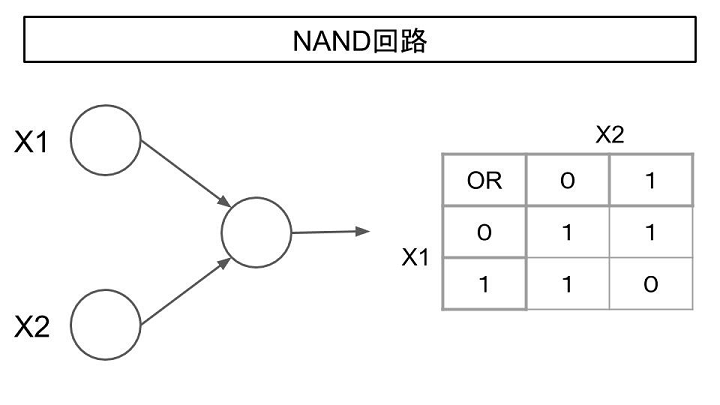
- ③NAND回路
NAND回路はAND回路を逆にしたもので(”N”ot”AND”でNAND)、X1、X2いずれも1を入力した場合に0、それ以外は1を出力します。
-
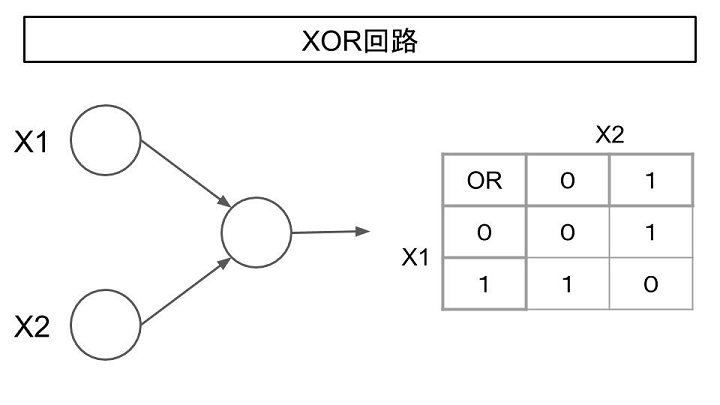
- ④XOR回路
XOR回路はX1、X2が異なる入力をした際に1、それ以外の場合は0を出力します。
さて、上記の①~③を以下のように組み合わせると④と同じ出力結果になります。

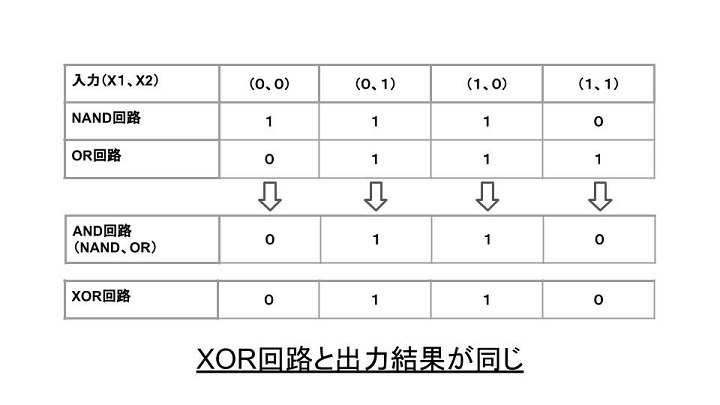
この組み合わせ層を増やしたモデルを『多層パーセプトロン』と言い、一番左の層を『入力層』、一番右の層を『出力層』、それ以外の層を『中間層』または『隠れ層』と呼びます。
数学的な工夫により、線形分離できない問題も既存のパーセプトロンモデルで解決できる可能性が出てきました。
この発見に加え、デビッド・ラメルハート氏とジェームズ・マクレランド氏が提唱した『バックプロパゲーションアルゴリズム』により人工知能は再度世間から注目を集めることになります。
逆算で考える『バックプロパゲーション(Backpropagation)』
単純なパーセプトロンモデルであれば、全ての重み付けを調整することも可能かもしれませんが、今回紹介したような多層化されたものや、入力層の数が増えたものを調整するのはとても大変で現実的ではありません。
この複雑なモデルでも効率的に重みづけを調整できる手法として考えられたのが『バックプロパゲーションアルゴリズム(誤差逆伝播法)』です。
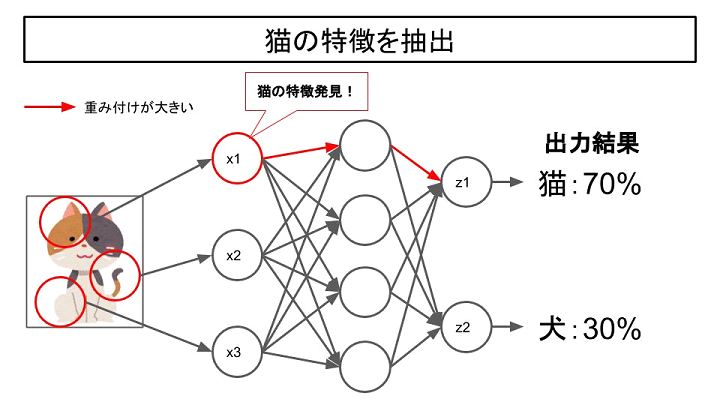
例えば、犬と猫を識別するモデルを作るとします。
バックプロパゲーションでは、まず大量の猫の画像を入力します。
正解は全て猫なので、出力された結果と正解とする値の誤差を調整していきます。
重み付けは最初ランダムな数値が割り振られ、重みの数値が大きいところほど出力結果に大きな影響を与えています。
正解と出力の誤差を小さくするような重みを逆に計算することで調整を繰り返していき、猫の特徴を捉えることができるモデルが出来上がります。
※実際に学習データを作ってみたい方はこちら
『OpenCVで機械学習をさせてみた!! 実装編第3回』
この手法のメリットは、人間が特徴を考えどこを認識するべきか指定するなど、これまでは手取り足取り教える必要があったものを、大量に画像を見せるだけでモデルが勝手に学習してくれる点にあります。
この発見により人工知能の可能性は再度見直されることとなりました。
しかし、これが発案された1986年の頃には学習に必要なデータ量がそろわず、期待するような結果が得られませんでした。
残念ながら再度冬の時代に突入する人工知能ですが、着実に技術の蓄積をしていき、2006年には一部の分野では人間の能力を凌駕する実績を上げていくこととなります。
続きはまた次回…
参考
EVENTS


