【脳トレ】ピタゴラスの定理を証明してみよう

最近、Youtubeで東大医学部在学中に司法試験も一発合格した、河野玄斗氏の勉強動画にハマっております。
とりわけ、算数・数学の面白さがすごい伝わってくるので、自分でもいろんな問題に挑戦したくなりますね。

東大や難関校の受験問題とかはなかなか難しいですが、公式とかは不要だけれど、ちょっと一工夫して解けるくらいが、クイズ感覚としても楽しめるかなと思います。というわけで、中学くらいに習ったピタゴラスの定理がなんで成り立つのか、脳トレ感覚でチャレンジしてみましょう。

ピタゴラスの定理ってなんだっけ

そんな方に、おさらいです。こちらをご覧ください。

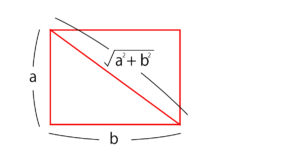
三角形の縦の長さをa、aと直行する底辺の長さをbと置いた時に、斜めの長さはaとbを二乗してルートを取ったものになるということです。
もっと砕くと、aとbが垂直のとき、斜めの長さを2回かけると、a、bをそれぞれ2回かけて足したものに等しいのです。さて、これがなぜ成り立つか。

意外と一筋縄ではいかなかったりする？

これ、いろんな証明方法があって、いくつかを中学くらいに習っていると思います。でも1から自分でやってみると、意外となかなかやり方が…
まあ補助線とか引きまくって、図形的にいろいろな角度から考えてみると、いつかはたどり着くのでしょう。

僕もさっそくやってみました。
まずは、aとbの四角形を作って、さらに縦横を90度回転させた四角形を左寄せし、さらに斜めの補助線を引いてみました。

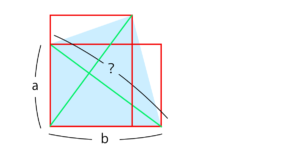
面積を使って考えてみる

三角形の斜めの長さの1つの求め方として、面積を使う方法があります。縦と横でも面積が求められるけど、斜めの長さだけでも面積が求められるよ、となれば、縦横の長さと斜めの長さの関係式が作れます。つまり、面積を通じて、縦横の長さから斜めの長さが求まるのです。

つぎに、面積を求めるには直角であることが大事です。縦×横で、面積はもとまりますからね。
それで、上で描いた緑の斜め線というのは、角度を計算すると、実は直交しているのです。ここでは端折るので、まだ分からないぞという方はじっくり考えてみてください。

台形の面積を求める

上の画像の緑線から出てきた、台形の面積を、aとbを使って求めてみます。そのままの形では求まらないので、工夫していくつかのパーツに分けます。パズル感覚で面白いですね。
下の画像のように、台形をいくつかのパーツに分けると簡単にも止まります。

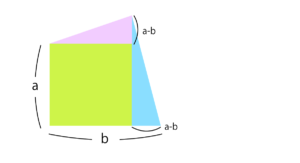
それぞれのパーツで面積を求めて、合計を計算…

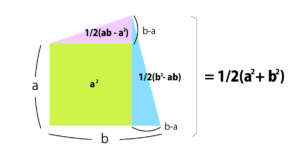
あとは関係式を作るだけ

台形の面積がもとまれば、もうカンタン。
先程の台形を、緑線と照らし合わせると、左斜めにいく線で上下にまっぷたつに割れることがわかります。（対称性）
で、緑線の長さはどちらも同じ長さで、かつ直行しているので、緑線の長さを？とおくと、面積が？を使った式で出てきます。

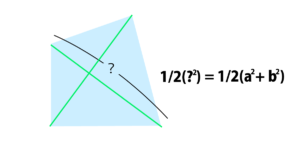
ということで、斜めの線の長さ？と、a、bとの関係式が出てくるのですね。

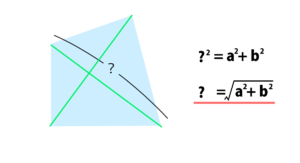
一工夫があらゆるところで役に立つ

こういう、一工夫おいて、なんとかして導いていくというのは、プログラミングに似ています。
論理的な思考力、というより工夫しながら試行錯誤なんとかやってみようですが、こういう考え方って大事ですよね。

大人になっても、算数や数学を勉強する大切さを感じました。