思い切ってニューラルネットワークを勉強してみよう(1)

こんにちは。山本睦月です。
今回は、難しそうで見て見ぬふりしてたものに思い切って触れてみるシリーズです。
記念すべき第1回のテーマは「AI(人工知能)を理解するうえで重要な要素技術である『ニューラルネットワーク』です」。
初回に相応しいとても難しそうなテーマですね。
しかしあえて私はこのテーマに立ち向かいます!
昨今のAIブームをどや顔で乗り切るために一緒に勉強していきましょう。
目次
まずは歴史を見てみよう
ニューラルネットワークの歴史をさかのぼっていくと、フランク・ローゼンブラット博士が1958年に発表した『パーセプトロン』という考え方が元になっていることがわかります。
ニューラルネットワークを理解する前にまずはパーセプトロンについて学んでいきましょう。
ローゼンブラット博士は心理学をはじめ、生物化学や神経生物学、行動学など幅広いテーマに精通していました。
そんな博士が注目したのが、眼球の仕組みです。
目に入った光は網膜で焦点を結び、集まったその光を視神経を通して脳に送ることで像として認識されます。
それはつまり、物を見るときは何かしらの情報処理が行われているということです。
目の前のコップを見たときに、そのコップそのものを見ているというよりは、視神経を伝わり届く一定の信号パターンを学習し「このパターンはコップだ」と判断していることになります。
ではこの視神経のモデルを作成し、結果を見ながら配線を調整すれば形を見分けることができる視神経モデルが作れるのではないか。と博士は考えました。
そのモデルがニューラルネットワークの元になる『パーセプトロン』です。
パーセプトロン
パーセプトロンは視神経の仕組みをモデル化したもので、簡単な図にしたものがこちらです。
図1.パーセプトロンのモデル
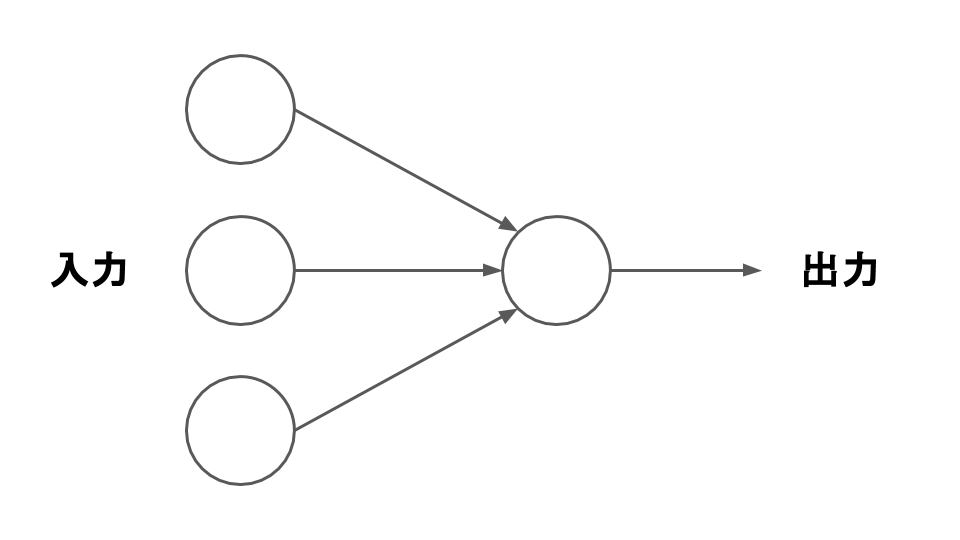
この図では入力を3つとしましたが、いくつに増やしてもOKです。とてもシンプルな形ですね。
入力された情報は定められたルールに乗っ取り結果を出力する仕組みとなっています。
ローゼンブラット博士はこの図にもう少し工夫を加えました。
それが『重み』という考え方です。
重みはそれぞれの入力が出力に及ぼす影響力を表したものです。
重みの数値が大きいほど出力への影響力が大きくなります。
図2.重み付きパーセプトロンのモデル
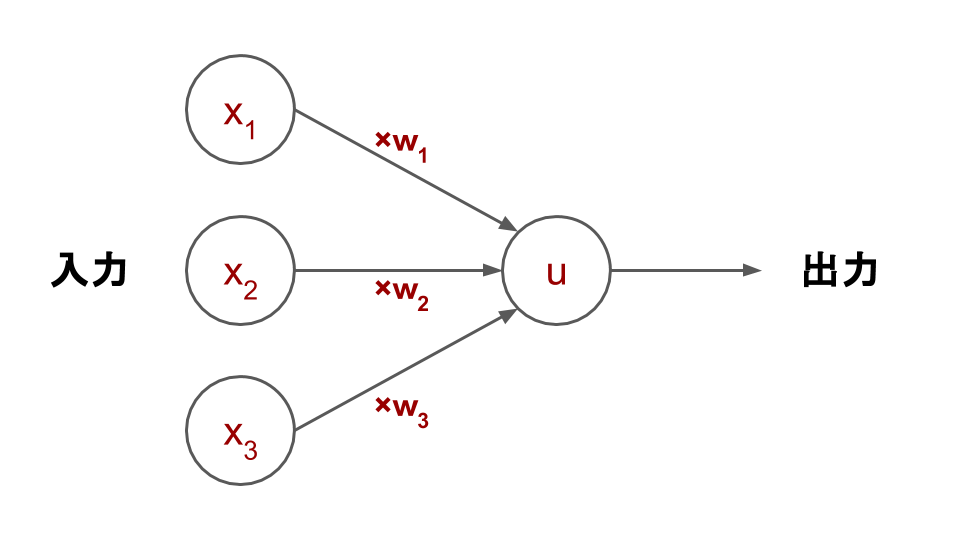
パーセプトロンの出力値は、この重みを計算に加えた入力値の和と閾値(しきいち)の大小比較で決定されます。
閾値とは判断を行うときに境目となる数値のことです。
例えば『20という閾値を用意し年齢を入力すると、入力された値と閾値を比べた大小でその人が未成年か成人しているかがわかる』といったようなことです。
重みという考え方は理想とする出力結果を得るために非常に重要な要素なのですが、
少しわかりにくいので実生活に置き換えて考えてみます。
今は土曜日の深夜1時。休日だったあなたは昼過ぎに起き一日中家でゴロゴロ。明日が休みなこともあり夜更かし中です。
テレビを見ているとおいしいラーメン屋特集をしています。
そして当然あなたは猛烈な空腹感に襲われます。その時あなたはカップラーメンを食べるか否かの選択に迫られたとします。
そんな状況で例えば下記のような3つの条件だとどんな結果になるでしょう?先ほどの図に当てはめて考えてみましょう。
図3.重み付きパーセプトロンのモデル(ラーメン)
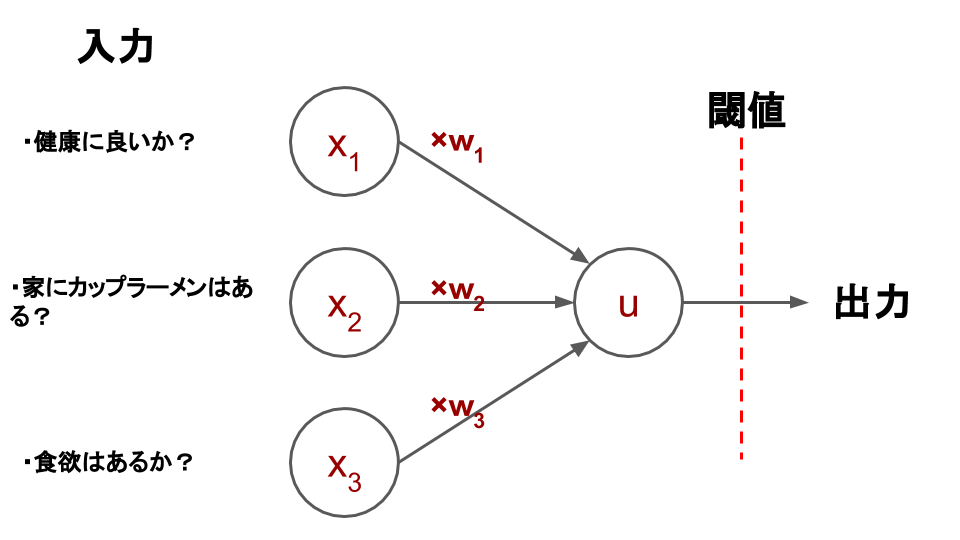
人によってどの条件に重みを置くかは違うと思います。
健康志向な人であればw1の重みが増え、他の項目の重みが減るので滅多なことでは深夜にラーメンを食べようなどという暴挙には出ないでしょう。
逆に本能に従い今を全力で生きる人なら、食欲に全振りしすぐにお湯を沸かすことでしょう。
これは単純化した例ですが、この条件を増やしたり重みづけや閾値を調整することでより理想の結果に近いものが得られることがわかります。
なんだ簡単じゃん!これで自分もAIマスターだ!と思われた方。残念ながらそうではないのです。
パーセプトロンのモデルが登場した時に多くの人が期待したと同時に数学者たちは落胆しました。
なぜならこのモデルには大きな問題点があったからです。
これは『XOR問題』と言われ、これによってAI(人工知能)は冬の時代に突入します。
この先はまた次回…
参考
EVENTS


