思い切ってニューラルネットワークを勉強してみよう(2)
※本記事は、未来技術推進協会ホームページにて2018年11月27日に掲載されたものです。
こんにちは。山本睦月です。
前回に引き続き、思い切ってニューラルネットワークを勉強してみようパート2です。
続きからの内容となりますので、パート1をご覧になってから本記事に進むのをオススメします。
※前回の記事はこちら
目次
前回のおさらい
人が物を見る仕組みから着想を得て作ったパーセプトロンモデル。これに『重み』という概念を加えることで、入力された情報からこちらが期待する出力を得ることができるモデルが出来ました。
心理学をはじめ、生物化学や神経生物学、行動学など幅広いテーマに精通したローゼンブラット博士によりこのモデルが発表されたとき、世界中が興奮しこの人工的な学習装置に期待をしました。しかし、このモデルには落とし穴があったのです!
パーセプトロンの限界
パーセプトロンのマーク1モデルでは、□や△などの簡単な図形を認識することができ、とても単純ではありますが、世界で初めて機械が知能の欠片(かけら)を手にした瞬間に世間は多いに盛り上がりました。「今は技術的な問題があり単純な図形だけしか認識できないが、今後技術が発展しモデルに使う部品が安価になれば飛躍的に進歩していく」と皆が期待していました。
そんな中、パーセプトロンには限界があると訴えたのが『人工知能の父』と呼ばれるマービン・ミンスキー氏です。
パーセプトロンが世に発表される少し前の1951年ごろ、ミンスキー氏は「迷路を歩き回りスタートからゴールまでを学習する機械『SNARC』」を開発しました。
パーセプトロンとSNARCは学習する基本構造が似ており、ミンスキー氏は一人冷静に「このモデルには限界がある」と直感的に感じ、それは直ぐに証明されることとなりました。
1963年、ミンスキー氏は数学者であるシーモア・パパート氏と知り合います。
パパート氏はミンスキー氏と同じようにパーセプトロンの限界を感じており、二人はすぐに意気投合しこのモデルの問題点の研究に取り掛かりました。
二人が導き出した結論は、パーセプトロンでは線形分離可能な問題しか学習できないということでした。
XOR問題
『線形分離可能な』とはどういった意味なのでしょうか?
例えば、男性と女性を分けるモデルを想像してみましょう。今回は身長と髪の長さである程度のグループに分けて男女に仕分けしてみます。
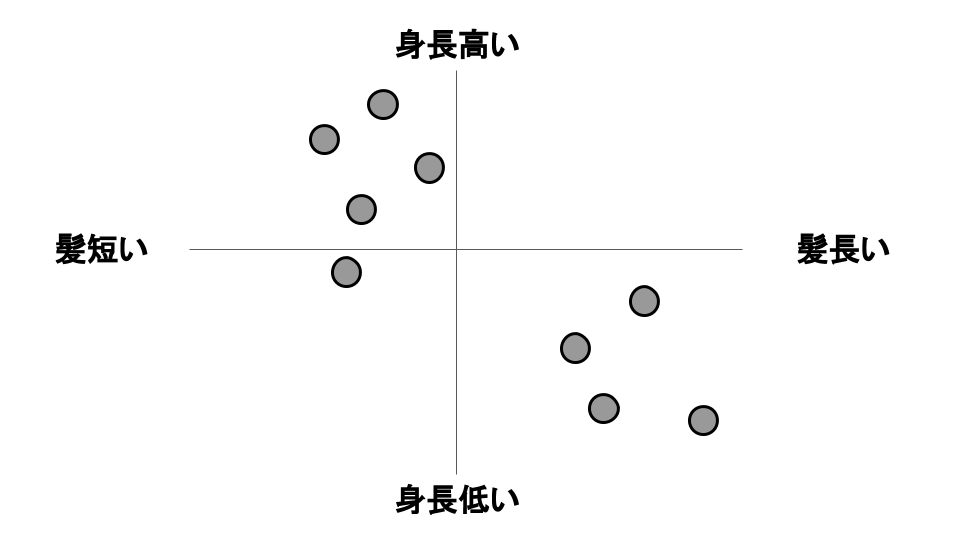
多少ばらつきはあるものの、おおよそ偏った分布になるかと思います。
ある特徴で切り分けられるものは各グループを直線で切り分けることができます。
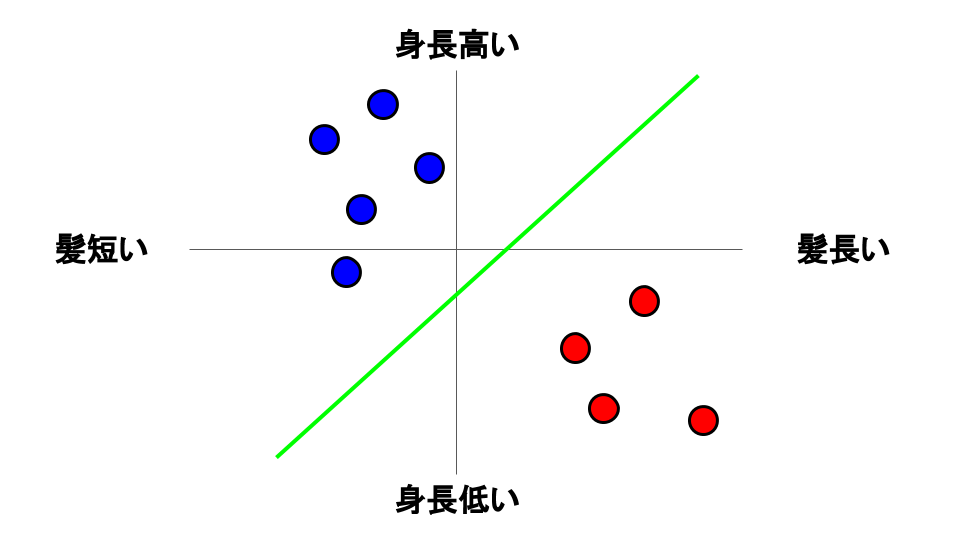
これが『線形分離可能な』問題です。
一見どんな条件でも出来そうな感じがします。ただ、上に示した男女を仕分けする問題ですら実は問題があります。世の中には身長が低い男性もいれば髪が短い女性もいるため、多くの例外が存在してしまうからです。
さて、この問題を論理演算に当てはめて整理してみましょう。
世の中の複雑な問題を解くには論理演算を避けて通ることはできません。
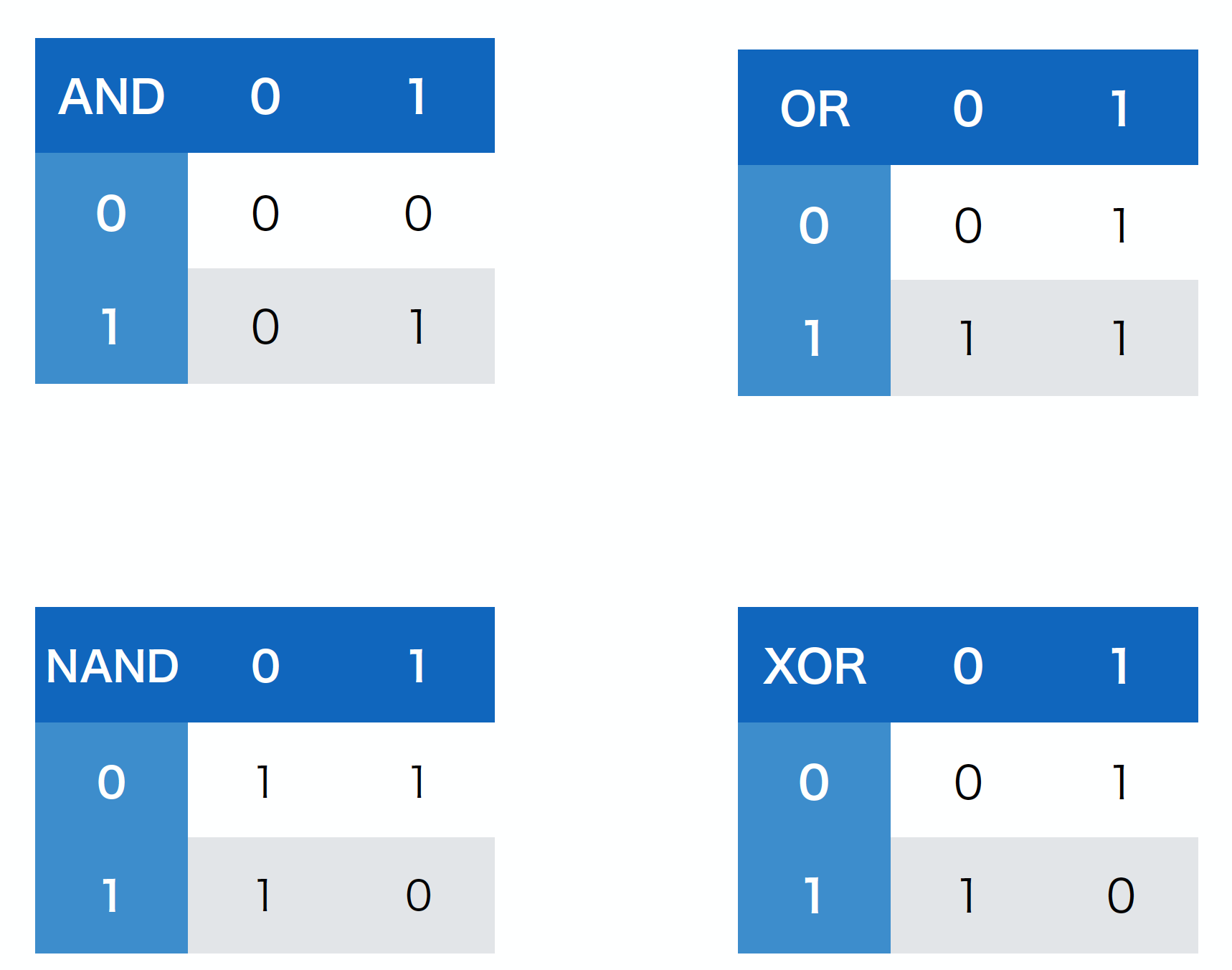
論理演算とは『AND・OR・NAND・XOR』などを基本とする、『真(1)』か『偽(0)』の入力値から一つの値を出力するものです。以下は4つの論理演算の出力結果とそれを2次関数のグラフ上に置いたものです。
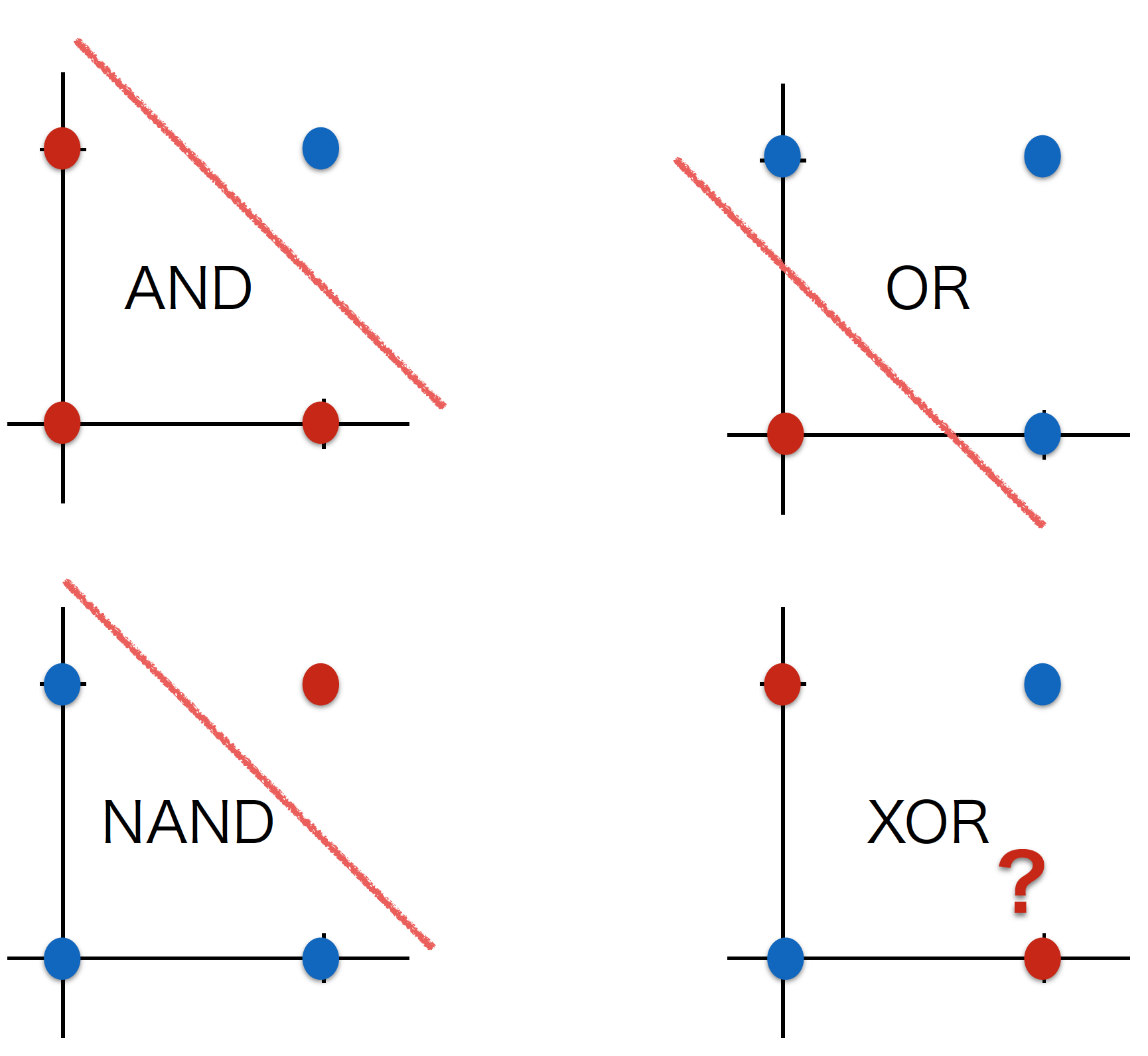
参照:『ハッカーの系譜(10)マービン・ミンスキー (9)人工知能「冬の時代」が到来』より引用
※AND…入力値A、入力値B両方が1の場合のみ1を出力。
※OR…入力値A、入力値Bいずれかが1であれば1を出力。
※NAND…AND型を否定した形。入力値A、入力値B両方が1の場合0。それ以外1を出力。
※XOR…入力値A、入力値Bが異なる値の時に1を出力。同じ時に0を出力。
パーセプトロンのモデルでは、こういった線形分離できない事象を抱えた問題を学習できないのです。これが『XOR問題』です。
1969年、ミンスキー氏とパパート氏はこの問題を1冊の本『パーセプトロン』にまとめ、世間に発表しました。
これによりあれだけ盛り上がっていたパーセプトロンの研究は一気に下火になってしまい、人工知能は冬の時代に入ります。
しかし、もちろん人工知能の歴史はここで終わりではありません。
1986年、デビッド・ラメルハート氏とジェームズ・マクレランド氏が提唱した、『バックプロパゲーションアルゴリズム』により人工知能は再度世間から注目を集めます。
後にこのモデルは『ディープラーニング』と呼ばれ社会を大きく変えていきます。
続きはまた次回…
参考
EVENTS


